JS Algorithms & Data Structures
javascript-algorithms 包含了多种基于 JavaScript 的算法与数据结构
README
JavaScript Algorithms and Data Structures
🇺🇦 UKRAINE IS BEING ATTACKED BY RUSSIAN ARMY. CIVILIANS ARE GETTING KILLED. RESIDENTIAL AREAS ARE GETTING BOMBED.
- Help Ukraine via National Bank of Ukraine
- Help Ukraine via SaveLife fund
- More info on war.ukraine.ua and MFA of Ukraine
This repository contains JavaScript based examples of many
popular algorithms and data structures.
Each algorithm and data structure has its own separate README
with related explanations and links for further reading (including ones
to YouTube videos).
_Read this in other languages:_
*☝ Note that this project is meant to be used for learning and researching purposes
only, and it is not meant to be used for production.*
Data Structures
A data structure is a particular way of organizing and storing data in a computer so that it can
be accessed and modified efficiently. More precisely, a data structure is a collection of data
values, the relationships among them, and the functions or operations that can be applied to
the data.
B - Beginner, A - Advanced
B Queue
B Stack
B Heap - max and min heap versions
A Trie
A Tree
A AVL Tree
A Segment Tree - with min/max/sum range queries examples
A Fenwick Tree (Binary Indexed Tree)
A Graph (both directed and undirected)
Algorithms
An algorithm is an unambiguous specification of how to solve a class of problems. It is
a set of rules that precisely define a sequence of operations.
B - Beginner, A - Advanced
Algorithms by Topic
Math
B Bit Manipulation - set/get/update/clear bits, multiplication/division by two, make negative etc.
B Binary Floating Point - binary representation of the floating-point numbers.
B Fibonacci Number - classic and closed-form versions
B Prime Factors - finding prime factors and counting them using Hardy-Ramanujan's theorem
B Primality Test (trial division method)
B Euclidean Algorithm - calculate the Greatest Common Divisor (GCD)
B Least Common Multiple (LCM)
B Sieve of Eratosthenes - finding all prime numbers up to any given limit
B Is Power of Two - check if the number is power of two (naive and bitwise algorithms)
B Complex Number - complex numbers and basic operations with them
B Radian & Degree - radians to degree and backwards conversion
B Horner's method - polynomial evaluation
B Matrices - matrices and basic matrix operations (multiplication, transposition, etc.)
B Euclidean Distance - distance between two points/vectors/matrices
A Square Root - Newton's method
A Liu Hui π Algorithm - approximate π calculations based on N-gons
A Discrete Fourier Transform - decompose a function of time (a signal) into the frequencies that make it up
Sets
B Cartesian Product - product of multiple sets
B Fisher–Yates Shuffle - random permutation of a finite sequence
A Power Set - all subsets of a set (bitwise and backtracking solutions)
A Permutations (with and without repetitions)
A Combinations (with and without repetitions)
A Longest Common Subsequence (LCS)
A Shortest Common Supersequence (SCS)
A Knapsack Problem - "0/1" and "Unbound" ones
A Maximum Subarray - "Brute Force" and "Dynamic Programming" (Kadane's) versions
A Combination Sum - find all combinations that form specific sum
Strings
B Hamming Distance - number of positions at which the symbols are different
B Palindrome - check if the string is the same in reverse
A Levenshtein Distance - minimum edit distance between two sequences
A Knuth–Morris–Pratt Algorithm (KMP Algorithm) - substring search (pattern matching)
A Z Algorithm - substring search (pattern matching)
A Rabin Karp Algorithm - substring search
Searches
B Jump Search (or Block Search) - search in sorted array
B Binary Search - search in sorted array
B Interpolation Search - search in uniformly distributed sorted array
Sorting
B Quicksort - in-place and non-in-place implementations
Linked Lists
Trees
B Depth-First Search (DFS)
B Breadth-First Search (BFS)
Graphs
B Depth-First Search (DFS)
B Breadth-First Search (BFS)
B Kruskal’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
A Dijkstra Algorithm - finding the shortest paths to all graph vertices from single vertex
A Bellman-Ford Algorithm - finding the shortest paths to all graph vertices from single vertex
A Floyd-Warshall Algorithm - find the shortest paths between all pairs of vertices
A Detect Cycle - for both directed and undirected graphs (DFS and Disjoint Set based versions)
A Prim’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
A Topological Sorting - DFS method
A Articulation Points - Tarjan's algorithm (DFS based)
A Bridges - DFS based algorithm
A Eulerian Path and Eulerian Circuit - Fleury's algorithm - Visit every edge exactly once
A Hamiltonian Cycle - Visit every vertex exactly once
A Strongly Connected Components - Kosaraju's algorithm
A Travelling Salesman Problem - shortest possible route that visits each city and returns to the origin city
Cryptography
B Polynomial Hash - rolling hash function based on polynomial
B Rail Fence Cipher - a transposition cipher algorithm for encoding messages
B Caesar Cipher - simple substitution cipher
B Hill Cipher - substitution cipher based on linear algebra
Machine Learning
B NanoNeuron - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
B k-NN - k-nearest neighbors classification algorithm
B k-Means - k-Means clustering algorithm
Image Processing
B Seam Carving - content-aware image resizing algorithm
Statistics
B Weighted Random - select the random item from the list based on items' weights
Evolutionary algorithms
A Genetic algorithm - example of how the genetic algorithm may be applied for training the self-parking cars
Uncategorized
B Square Matrix Rotation - in-place algorithm
B Jump Game - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
B Unique Paths - backtracking, dynamic programming and Pascal's Triangle based examples
B Rain Terraces - trapping rain water problem (dynamic programming and brute force versions)
B Recursive Staircase - count the number of ways to reach to the top (4 solutions)
B Best Time To Buy Sell Stocks - divide and conquer and one-pass examples
Algorithms by Paradigm
An algorithmic paradigm is a generic method or approach which underlies the design of a class
of algorithms. It is an abstraction higher than the notion of an algorithm, just as an
algorithm is an abstraction higher than a computer program.
Brute Force - look at all the possibilities and selects the best solution
B Rain Terraces - trapping rain water problem
B Recursive Staircase - count the number of ways to reach to the top
A Travelling Salesman Problem - shortest possible route that visits each city and returns to the origin city
A Discrete Fourier Transform - decompose a function of time (a signal) into the frequencies that make it up
Greedy - choose the best option at the current time, without any consideration for the future
A Dijkstra Algorithm - finding the shortest path to all graph vertices
A Prim’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
A Kruskal’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
Divide and Conquer - divide the problem into smaller parts and then solve those parts
B Euclidean Algorithm - calculate the Greatest Common Divisor (GCD)
B Tree Depth-First Search (DFS)
B Graph Depth-First Search (DFS)
B Matrices - generating and traversing the matrices of different shapes
B Best Time To Buy Sell Stocks - divide and conquer and one-pass examples
A Permutations (with and without repetitions)
A Combinations (with and without repetitions)
Dynamic Programming - build up a solution using previously found sub-solutions
B Rain Terraces - trapping rain water problem
B Recursive Staircase - count the number of ways to reach to the top
B Seam Carving - content-aware image resizing algorithm
A Levenshtein Distance - minimum edit distance between two sequences
A Longest Common Subsequence (LCS)
A Bellman-Ford Algorithm - finding the shortest path to all graph vertices
A Floyd-Warshall Algorithm - find the shortest paths between all pairs of vertices
Backtracking - similarly to brute force, try to generate all possible solutions, but each time you generate next solution you test
if it satisfies all conditions, and only then continue generating subsequent solutions. Otherwise, backtrack, and go on a
different path of finding a solution. Normally the DFS traversal of state-space is being used.
B Power Set - all subsets of a set
A Hamiltonian Cycle - Visit every vertex exactly once
A Combination Sum - find all combinations that form specific sum
Branch & Bound - remember the lowest-cost solution found at each stage of the backtracking
search, and use the cost of the lowest-cost solution found so far as a lower bound on the cost of
a least-cost solution to the problem, in order to discard partial solutions with costs larger than the
lowest-cost solution found so far. Normally BFS traversal in combination with DFS traversal of state-space
tree is being used.
How to use this repository
Install all dependencies
- ```
- npm install
- ```
Run ESLint
You may want to run it to check code quality.
- ```
- npm run lint
- ```
Run all tests
- ```
- npm test
- ```
Run tests by name
- ```
- npm test -- 'LinkedList'
- ```
Troubleshooting
In case if linting or testing is failing try to delete the node_modules folder and re-install npm packages:
- ```
- rm -rf ./node_modules
- npm i
- ```
Also make sure that you're using a correct Node version (>=14.16.0). If you're using nvm for Node version management you may runnvm use from the root folder of the project and the correct version will be picked up.
Playground
You may play with data-structures and algorithms in ./src/playground/playground.js file and write
tests for it in ./src/playground/__test__/playground.test.js.
Then just simply run the following command to test if your playground code works as expected:
- ```
- npm test -- 'playground'
- ```
Useful Information
References
Big O Notation
Big O notation is used to classify algorithms according to how their running time or space requirements grow as the input size grows.
On the chart below you may find most common orders of growth of algorithms specified in Big O notation.
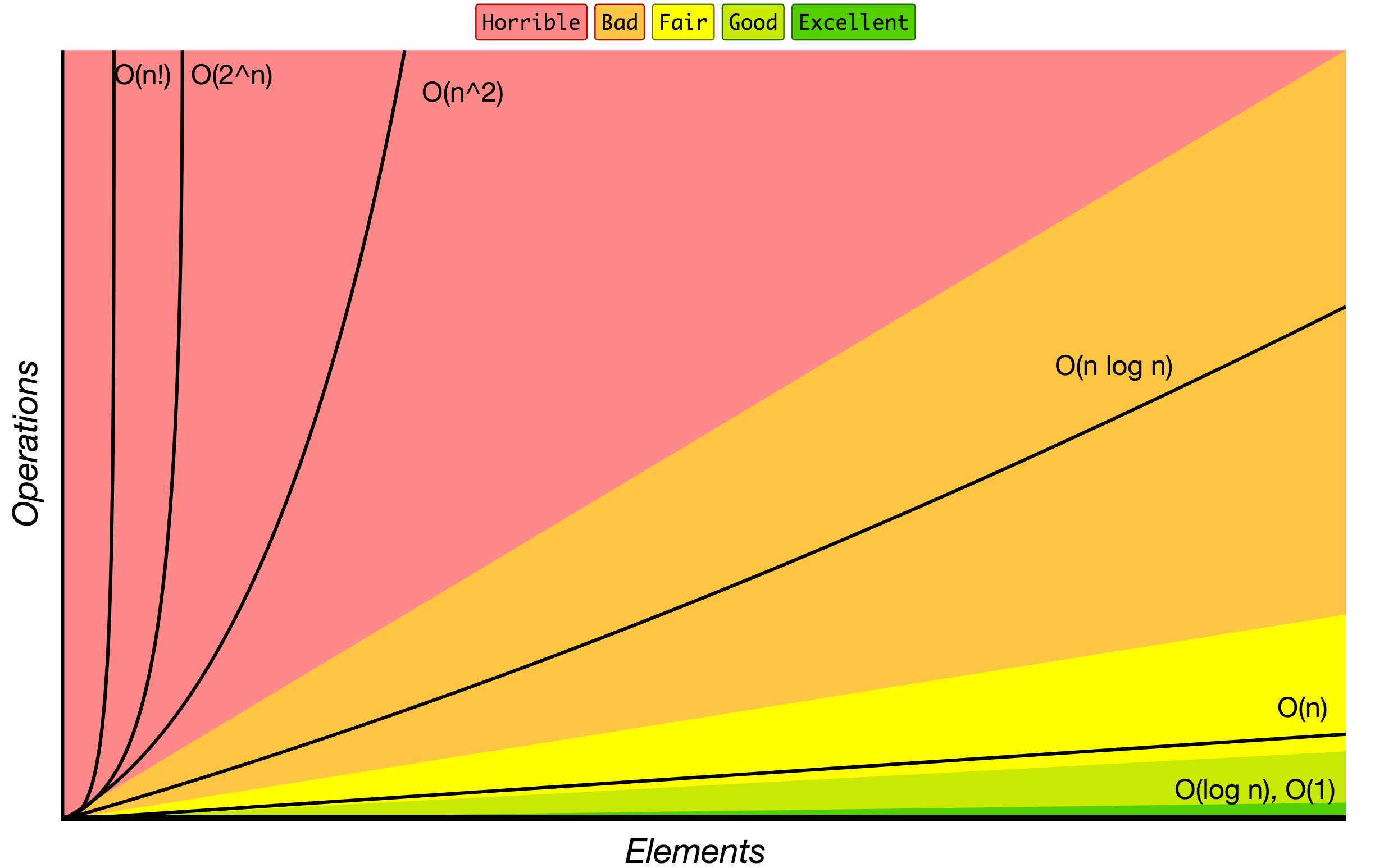
Source: Big O Cheat Sheet.
Below is the list of some of the most used Big O notations and their performance comparisons against different sizes of the input data.
| Big | Type | Computations | Computations | Computations |
|---|---|---|---|---|
| -------------- | ----------- | ---------------------------- | ----------------------------- | ------------------------------- |
| **O(1)** | Constant | 1 | 1 | 1 |
| **O(log | Logarithmic | 3 | 6 | 9 |
| **O(N)** | Linear | 10 | 100 | 1000 |
| **O(N | n | 30 | 600 | 9000 |
| **O(N^2)** | Quadratic | 100 | 10000 | 1000000 |
| **O(2^N)** | Exponential | 1024 | 1.26e+29 | 1.07e+301 |
| **O(N!)** | Factorial | 3628800 | 9.3e+157 | 4.02e+2567 |
Data Structure Operations Complexity
| Data | Access | Search | Insertion | Deletion | Comments |
|---|---|---|---|---|---|
| ----------------------- | :-------: | :-------: | :-------: | :-------: | :-------- |
| **Array** | 1 | n | n | n | | |
| **Stack** | n | n | 1 | 1 | | |
| **Queue** | n | n | 1 | 1 | | |
| **Linked | n | n | 1 | n | | |
| **Hash | - | n | n | n | In |
| **Binary | n | n | n | n | In |
| **B-Tree** | log(n) | log(n) | log(n) | log(n) | | |
| **Red-Black | log(n) | log(n) | log(n) | log(n) | | |
| **AVL | log(n) | log(n) | log(n) | log(n) | | |
| **Bloom | - | 1 | 1 | - | False |
Array Sorting Algorithms Complexity
| Name | Best | Average | Worst | Memory | Stable | Comments |
|---|---|---|---|---|---|---|
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
| **Bubble | n | n2 | n2 | 1 | Yes | | |
| **Insertion | n | n2 | n2 | 1 | Yes | | |
| **Selection | n2 | n2 | n2 | 1 | No | | |
| **Heap | n log(n) | n log(n) | n log(n) | 1 | No | | |
| **Merge | n log(n) | n log(n) | n log(n) | n | Yes | | |
| **Quick | n log(n) | n log(n) | n2 | log(n) | No | Quicksort |
| **Shell | n log(n) | depends | n (log(n))2 | 1 | No | | |
| **Counting | n | n | n | n | Yes | r |
| **Radix | n | n | n | n | Yes | k |
Project Backers
ℹ️ A few more projects and articles about JavaScript and algorithms on trekhleb.dev
 探客时代
探客时代

